Math Projects

Project-Based Learning 

Key Questions

Projects result from students' attempts to answer essential questions.  They can take many forms: products, presentations, performances.  They might fit any of three structures: interpersonal, information sharing, or problem-solving.  When selecting an existing project, or creating one of your own, consider the following:

1. Is the project devoted only to mathematics (or a single subject area), or is there a link to other curricular areas?

2. Is the project tied to standards for the curricular areas addressed, such as those from the National Council of Teachers of Mathematics and the National Education Technology Standards?

3. Does the project come with classroom instructional materials (e.g., teacher resources, student activities, rubrics and assessment tools)?

4. Can all students in your class participate?  Projects should not be reserved for your talented and gifted students, as all students should be able to benefit.

5. What is the total time for project completion?

6. Is the project collaborative in nature?  A collaborative project, particularly involving students outside your own school setting, will take more time and monitoring to help students learn how to be a part of a team and communicate appropriately with others.

7. How will students benefit both academically and personally from their involvement in the project?  Consider that when students interact with other students and experts across the country or internationally, they get a broader feel for diversity.  Their participation in an actual real world activity might encourage them to do their best work, and see the relevance of mathematics in their daily lives.  If students have input into project selection, and like the topic, they will tend to become more involved and excited about their learning.

8. Is there a cost involved to participate?

The Methodology

These resources are for those who need to know more before engaging in projects and inquiry based learning:

Inquiry and Information and Communication Technologies from the Galileo Educational Network Association includes a series on the nature of inquiry-based learning.  Learn about what inquiry is all about, choosing a topic, essential questions, inquiry and assessment, and get classroom examples of projects for elementary, middle,  and secondary students and a rubric for assessing inquiry projects. 

Intel® Innovation in Education has a three-hour hands-on free workshop on project-based learning, which has a guided self-study module as an accompaniment.  Learn about this method as you examine It's a Wild Ride, an extended interdisciplinary project that studies roller coaster design in science, mathematics, and language arts classrooms.  A free video and Web-based resource enhance this case study experience.

Project Based Learning is a two- to three- hour learning module from the George Lucas Educational Foundation.  Find out what project based learning is, why it is important, how it works, and get some supporting resources.

Project Approach to Teaching and Learning in school addresses the foundation theory for using projects, strategic planning, and project development structure.  This is an award winning site by Sylvia Chard of the University of Alberta, Canada. You might also be interested in the interview of Dr. Chard addressing project-based learning, which is available from Edutopia of the George Lucas Educational Foundation.

Project Centre @2Learn.ca provides several entry points to learn what it take to make a successful telecollaborative project happen.  Get the how to's, read about teacher experiences, select a project model, learn the sequence in a project process.  There are numerous resources, project tools, readings and research, and a glossary.  Then explore or join projects--hundreds are in the database--or create your own project. 

In Using the Internet to Promote Inquiry-Based Learning, authors D. Jakes, M. Pennington, and H. Knodle describe a structured approach to inquiry-based learning that uses the World Wide Web.  They address an intuitive 8-step process that begins with an essential question and ends with a knowledge product produced by students, typically completed in a cooperative setting. They discuss the skills that students and teachers require to make inquiry-based learning and the Internet a successful endeavor; and the components of a Project Page, which include the scenario, task, resources, product students will build, and assessment.

Back to top

Projects on the Web

If you wish to become involved with project-based learning, it might be easier to start by participating in one that has been designed by others.

Ask Dr. Math is an e-mail questioning and answering service for math students and their teachers.  Dr. Math also gathers the best questions and answers into a searchable archive organized by grade level (elementary, middle school, high school) and topic (exponents, infinity, polynomials, etc.).

CIESE, the Center for Innovation in Engineering and Science Education, sponsors and designs projects for elementary, middle, and high school students that utilize real time data available from the Internet, and global collaboration with peers and experts. Each project has a brief description and links to the National Science Standards and NCTM math standards it supports.  All focus on science and mathematics, but have many interdisciplinary aspects as well, including social studies, language arts, art, and foreign languages.   See the Math and Science Projects at http://www.ciese.org/mathprojects/.  Projects have received accolades from the U.S. Department of Education, Discovery Channel, the National Science Teachers Association, and more.  Extensive teacher resources are available to support technology integration, professional development, and Internet safety.  Links to Real Time Data Sites are particularly useful.

Data Library from the Math Forum contains lists of on-going data-sharing projects as well as downloadable Excel and Clarisworks spreadsheets along with other sources of data on the web.

Electronic Emissary from the University of Texas connects your students to projects involving professional experts and uses e-mail for mentoring.  The project went online in 1993 and is believed to be  the longest-running Internet-based telementoring and research effort serving K-12 students and teachers around the world. Project-based online conversations typically range in length from 6 weeks to a full academic year, as students' needs and interests dictate.

Global Schoolhouse is a clearinghouse of over 900 online collaborative projects, organized by curriculum area, grade, technologies used, and project date.  Join an existing project or announce one of your own.  The database contains at least 250 projects addressing math.

GLOBE (Global Learning and Observations to Benefit the Environment) is a worldwide hands-on, primary and secondary school-based science and education program.  Students use the scientific method to create hypotheses, analyze data, draw conclusions and report their results through the Internet.  They take scientifically valid measurements in the fields of atmosphere, hydrology, soils, and land cover/phenology - depending upon local curricula.  GLOBE trains teachers to help students improve their achievement in science and math, and in the use of computer and network technology.

Hands-On Math Projects, Volume 2, by Carolyn S. Carter with Sara Cohen, Marian Keyes, Patricia S. Kusimo, and Crystal Lunsford, contains two chapters devoted to "Projects That Help Middle-School-Age Youth Discover the Science and Mathematics in Everyday Life."  The Mathematics of Quilting exposes learners to plane geometry, symmetry, and tessellations.  In Making Art through Mathematics, learners explore Cartesian coordinates, 2-D and 3-D geometry, measurement, symmetry, and volume.  This is a pdf document.

HOT Math!--Hands-on Tasks in Math, by Pauline Vos at the University of Twente in the Netherlands, offers activities for students in middle and high school that link math to other subject areas and learners' experiences.  Topics include "angles, symmetry, scale drawing, balance algebra, tables, combinations, statistics, probability, reasoning, finding rules and formulas, problem solving" and so on.  Activities take about 30 minutes each and are appropriate for group work.  Ideas for higher order cognitive skills, class discussion, and assessment are provided with each task.

iEARN (International Education and Resource Network) "enables young people to use the Internet and other new technologies to engage in collaborative educational projects that both enhance learning and make a difference in the world."  Math projects, for example, include Mathematics and Agriculture (ages 10+), Connecting Math to Our Lives (all ages), and Mathematics Virtual Learning Circle (all ages).  iEARN offers both face-to-face and online professional development workshops and courses for educators seeking to integrate online global project work into their classrooms.  Workshops include the technical, collaborative and organizational skills needed to participate.

Los Angeles County Office of Education, Center for Distance and Online Learning, has numerous subject matter resources, classroom projects (completed and ongoing), computer technology resources (e.g., lesson plans, webquests), teacher tips, standards/assessment documents, and more.  Definitely worth the look. 

Making Mathematics includes open-ended research projects suitable for grades 7-12, which was supported by a grant from the National Science Foundation during 199-2002.  Math projects, which remain online for replication, are rated from 1 (no algebra) to 4 (advanced algebra and beyond).  Projects contain the problem statement, prerequisites, warm-up problems, hints, resources, teacher notes, extension problems, results.  Additional resources include a teacher handbook with advice and activities for teaching research skills, a mentor handbook, and mathematics tools with important supporting content regarding proof, number theory, Pascal's triangle, Geometry of complex numbers, Iteration, and Numbers and Infinity.

MathMovesU is a new initiative from Raytheon Company to make math and science more interesting for middle school students.  See how math is at work with various careers from the viewpoints of several celebrities ranging from top pro sports figures to the video game designer, concert tour manager, fashion designer, roller-coaster designer, ER doctor, and the Spy Museum Director.  Participate in the weekly math challenge, apply for scholarships, and get grants for your school.

Math TV Problem Solving Videos is an innovation learning project for middle school students.  According to Noreen McGrath (email communication July 27, 2004), the grade 6 math teacher who recommended this site, "The goal of the project is to get middle school students excited about problem solving in mathematics.  Students send in word problems which, if selected, are incorporated into a video which shows a very detailed, step-by-step explanation of how to solve the problem.  The narrator of the fictional Math TV show, Infinity Quick, emphasizes a logical approach to problem solving and utilizes a variety of strategies.  At the end of the video students are invited to try a similar, interactive word problem complete with helpful hints and tools."  Math TV indicates that the practice area has an online calculator and notepad for testing ideas and making a drawing.  Whole numbers, fractions, percentages, ratios, probability, algebra and geometry are among topics explored.

Multimedia Mania "is an annual award program sponsored by ISTE HyperSig to promote the collaboration of K-12 teachers and students in creating multimedia projects related to any class or coursework. This awards program is for students and teachers who use multimedia to teach and learn in a specific content area (e.g. math, science, social studies, language arts, art, music, physical education, ESL, etc.) Students are invited to share their work with an international audience by creating dynamic multimedia projects related to any class or coursework. Multimedia Mania winners usually come from classrooms in which technology is used as a tool to teach and learn any standard curriculum. Teachers may coach and advise, but work must be completed by students in grades K-12."  Check out this year's program!

National Math Trail: This project receives support from the US Department of Education's Star Schools program, through the Satellite Education Resources Consortium (SERC), and NEC Foundation.  K-12 teachers and students share the math that exists in their own environments. "Students explore their communities and create one or more math problems that relate to what they find. Teachers submit the problems to the National Math Trail site, along with photos, drawings, sound recordings, videos--whatever can be adapted to the Internet."  Submissions are posted to the site, and indexed according to grade level and math topic.  The site clearly addresses NCTM standards, including connections, communication, problem solving.

NickNacks Telecollaborate: Site contains links to numerous collaborative projects and how-to information.

Statistics: A Curiosity Factor is a project suitable for use with middle school or high school students studying the concept of collecting and analyzing data.  It also provides an introduction to survey research.

Teacher Tap: WebQuests.  If you are not confident about designing your own WebQuest, this resource will help you to locate and evaluate WebQuests by grade level and content area that have been designed by others. 

ThinkQuest Internet Challenge Library contains over 5,000 projects build by kids for kids.  Math subcategories include geometry, chaos theory, fractals, algebra, trigonometry, statistics, probability, pre-calculus, calculus, arithmetic, puzzles, cryptography, real life uses, olympiads, and history topics related to math. 

The Webquest Locator from the Greater Essex County District School Board in Canada is an online database of teacher created webquests from a wide variety of sources.  The site has been recognized by the NEA.  With over 850 references all categorized by grade level or correlation to the Ontario Curriculum, this is a handy starting place to look for classroom Internet activities. 

Wonders of Math from the Galileo Educational Network Association and Mt. Royal College in Calgary, Alberta, Canada contains a number of inquiry based activities with special sections devoted to "That's a Good Problem," puzzles with printable worksheets, elementary and secondary project investigations, Japanese Lesson Study, and additional resources. 

Back to top

Design Your Own Project or WebQuest

Want to design your own project or have students design their own curriculum-based multimedia projects?  

Increase learning with student multimedia projects.  If you are planning your own project, consider using the following tools from the Buck Institute for Education:

• Project Planning Form begins with the end in mind and a driving question to guide development.
• The Tuning Protocol contains a process to help small groups to discuss project plans at the beginning or findings as the project progresses, and reveal potential problems.
• Implementation Tools include a weekly planning sheet, planning brief, learning log, investigation brief, product brief, presentation brief, research log, project milestones, progress report following an investigation, all of which are intended to help students plan, monitor, and evaluate their work.
• Examples of rubrics, templates, and criteria for their creation: accessing information, selecting information, processing information, composing a presentation, making a presentation, individual task management, individual time management, group task and time management, group process.  A form for project grading and a blank rubric are included.

Want to create a telecollaborative project from scratch?

Project Centre @2Learn.cacontains a guide to creating telecollaborative projects, checklists for project development, and a tool to help you build a webpage for your project.  There is also a searchable database, if you are looking for ideas for K-12 or post-secondary mathematics projects.

What is a WebQuest?  According to Tom March in The Learning Power of WebQuests (Educational Leadership, December 2003/January 2004), there are six elements of a real WebQuest:

1. a scaffolded learning experience,
2. use of links to essential resources on the World Wide Web,
3. an authentic task to motivate students' investigation,
4. open-ended questions,
5. development of individual expertise, and
6. participation in a group process that transforms newly acquired information into a more sophisticated understanding. 

Some activities may be designed to use Internet resources to produce a product, but can't be classified as WebQuests.  These non-Webquest activities are those that enable learners to gather  information that can go from a browser directly to a product without altering or involving students' understanding, and reflection on their own metacognitive processes.  To assess the real value of a WebQuest, ask "Is this WebQuest real, rich, and relevant?" 

Webquest Tutorials, Templates, and Project Examples

MyProjectPages.com will help you to "create structured online inquiry-based learning activities for the courses you teach."  Use their "wizard interface to design projects without any knowledge of Web publishing. Edit projects at any time using our easy editing interface."  Your project will be added to their searchable gallery of projects, which can also give you new ideas.

Creating a WebQuest: It's Easier Than You Think! from Education World

Math WebQuests Examples for elementary, middle, and high school students are at L. McCoy's (Wake Forest University) site.

Tom March/ozline.com Tom March, one of the original developers of WebQuests, has his own site with his blog, numerous articles and examples of WebQuests.

The WebQuest Page training materials.  This site is maintained by Bernie Dodge, who with Tom March developed this model at San Diego State University in 1995. 

WebQuest 101 by the Network for Instructional TV has a tutorial with examples to help you get started.

WebQuest Template from Cape Breton-Victoria, Regional School Board, Education Centre.  Includes directions within the sections: Introduction, Task, Process, Evaluation (Rubric design), and Conclusion.

Back to top

Project Assessment

If you decide to create your own project, including one that might involve multimedia, assessment will play a key role. Learn how to create rubrics to help measure quality and student performance on projects with these additional resources. Or, use an existing rubric. 

The following existing rubrics from various locations might be of value in projects:

• Collaboration Rubric
• Oral Presentation Rubric
• Website Design Rubric
• Rubric for Evaluating WebQuests from Bernie Dodge
• Rubrics for Assessment from University of Wisconsin-Stout: video and multimedia production, podcasts, web page and ePortfolios, math, oral presentations, and more

RubiStar provides 10 steps to creating a rubric.  If you don't have time to create your own, use the customizable templates from nine categories.  Math templates are provided for graphing and problem solving.  After your students have done the project and the rubric has been used to grade it, you can use RubiStar to analyze the data to determine which items are problematic for the class as a whole.  

Teach-nology's Rubric Makers allow you to make grading rubrics by filling out a simple form. The materials are made instantly and can be printed directly from your computer.  You can also customize your own rubric.  Rubrics of interest include homework, class participation, math projects, oral presentations, WebQuests, team work, writing, research reports, and reading. 

The Scoring Guide for Student Projects is also an excellent resource developed at the North Central Regional Educational Laboratory (MCREL).  This Web tool helps teachers evaluate student products that are created with technology. It focuses on the student’s content knowledge and effective technology use.  

Student Checklist and Judges' Rubric from Multimedia Mania, which is an annual award program sponsored by ISTE HyperSig.

 

Seek Permission! David Warlick of Landmarks for Schools (http://landmark-project.com/index2.php) reminds teachers and students to seek permission when using information from web sites designed by others.  He has provided simple to use Permission Templates for this purpose, which will automatically go to the author or web master of the site you wish to use in instruction or for a school project.  Use his Citation Machine to automatically create references in either APA or MLA format.  Students then can cut and paste those references into their projects.

References: 

Project Based Learning. Buck Institute for Education: http://www.bie.org/pbl/index.php

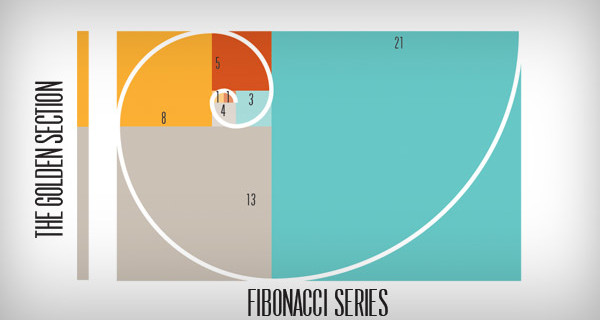March, T. (December 2003/January 2004). The learning power of webquests. Educational Leadership, 61(4), 42-47.

Back to top

Learn about the technical side of creating multimedia projects, including working with images and video.

See CT4ME Technology Integration